빅데이터
- weka 설치
- Data mining tool
- Anaconda 설치
Clustering
- 데이터가 주어지고, 원하는 개수만큼 데이터를 그룹으로 만드는 것
- 그룹내의 데이터는 비슷한 내용
Hierarchical Clustering(계층 분석)
-
Single Link
- 계층 적 클러스터링에서 두 개의 가장 가까운 멤버가 가장 작은 두 클러스터 (또는 : 최소 페어 와이즈 거리 가 가장 작은 두 클러스터)를 각 단계에서 병합
- O(n^2)
- weka를 이용한 single link
/img/in-post/
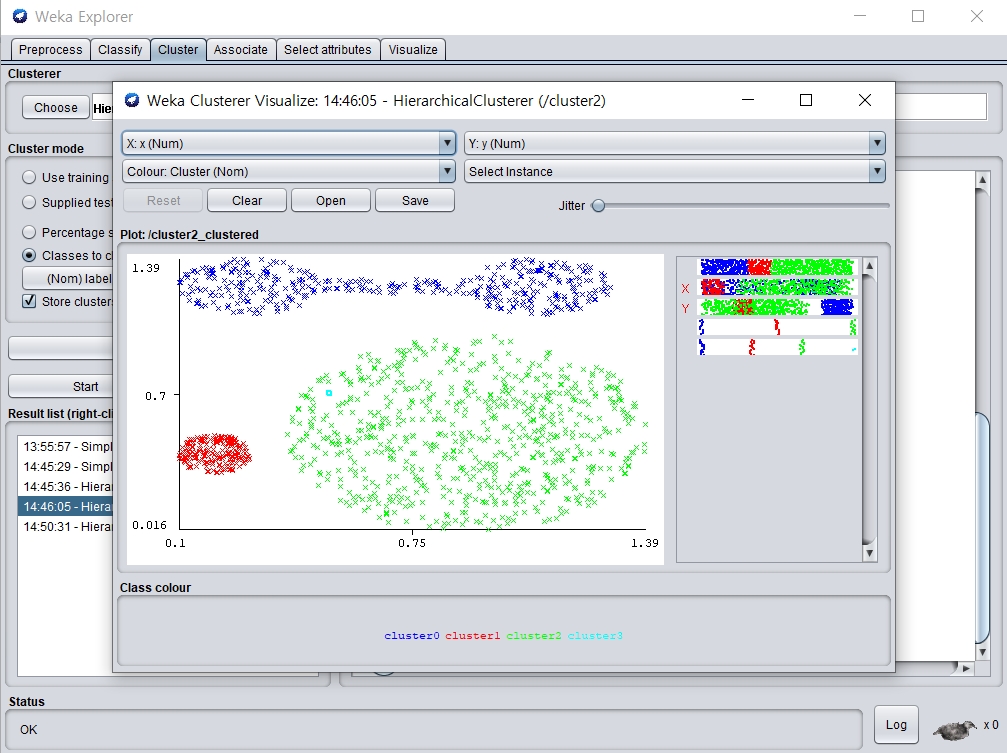
-
Complete Link
- 계층 적 클러스터링에서 합병이 가장 작은 두 클러스터를 각 단계에서 병합(또는 : 최대 쌍 거리 가 가장 작은 두 클러스터 )
- O(n^2 log n)
- weka를 이용한 complete link
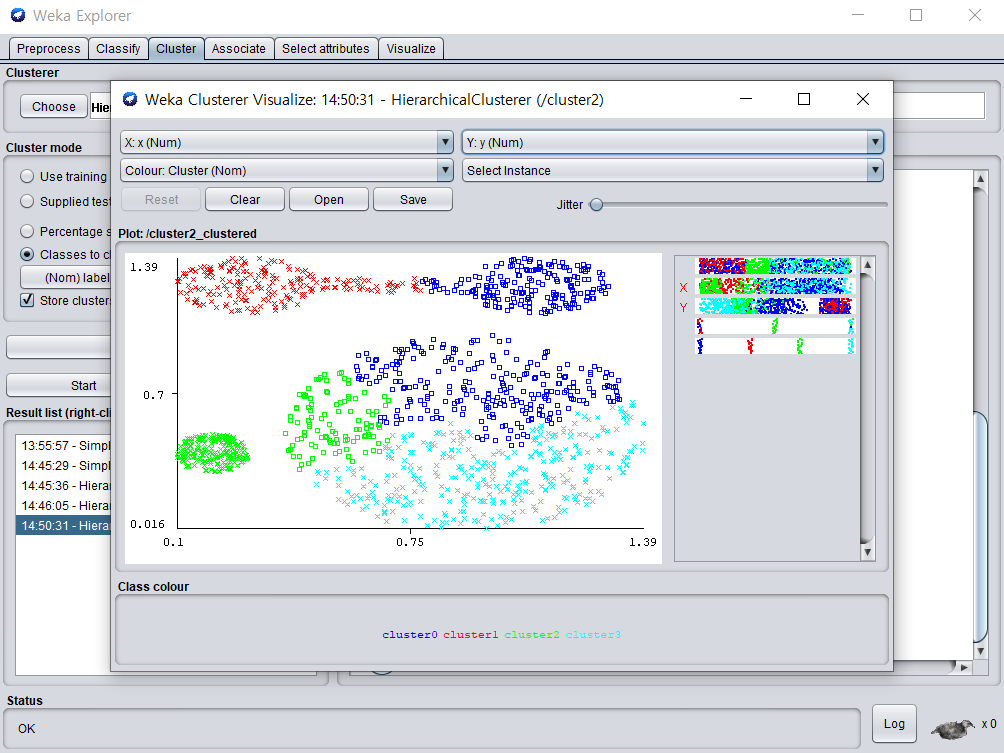
https://nlp.stanford.edu/IR-book/completelink.html
- 코드로 작성해보기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
X = df.values
for i, linkage in enumerate(('single', 'complete')):
clustering = AgglomerativeClustering(
linkage=linkage, n_clusters=4)
y_pred = clustering.fit_predict(X)
plt.figure(i + 1, figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y_pred, s=4)
plt.title(linkage)
plt.show()
- 결과
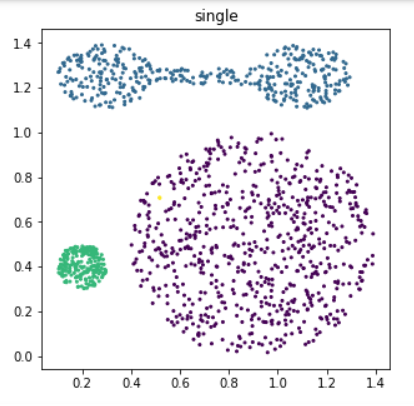
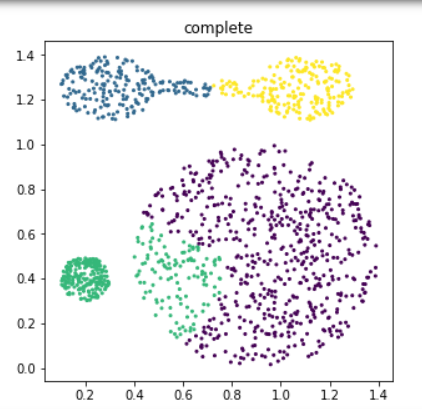
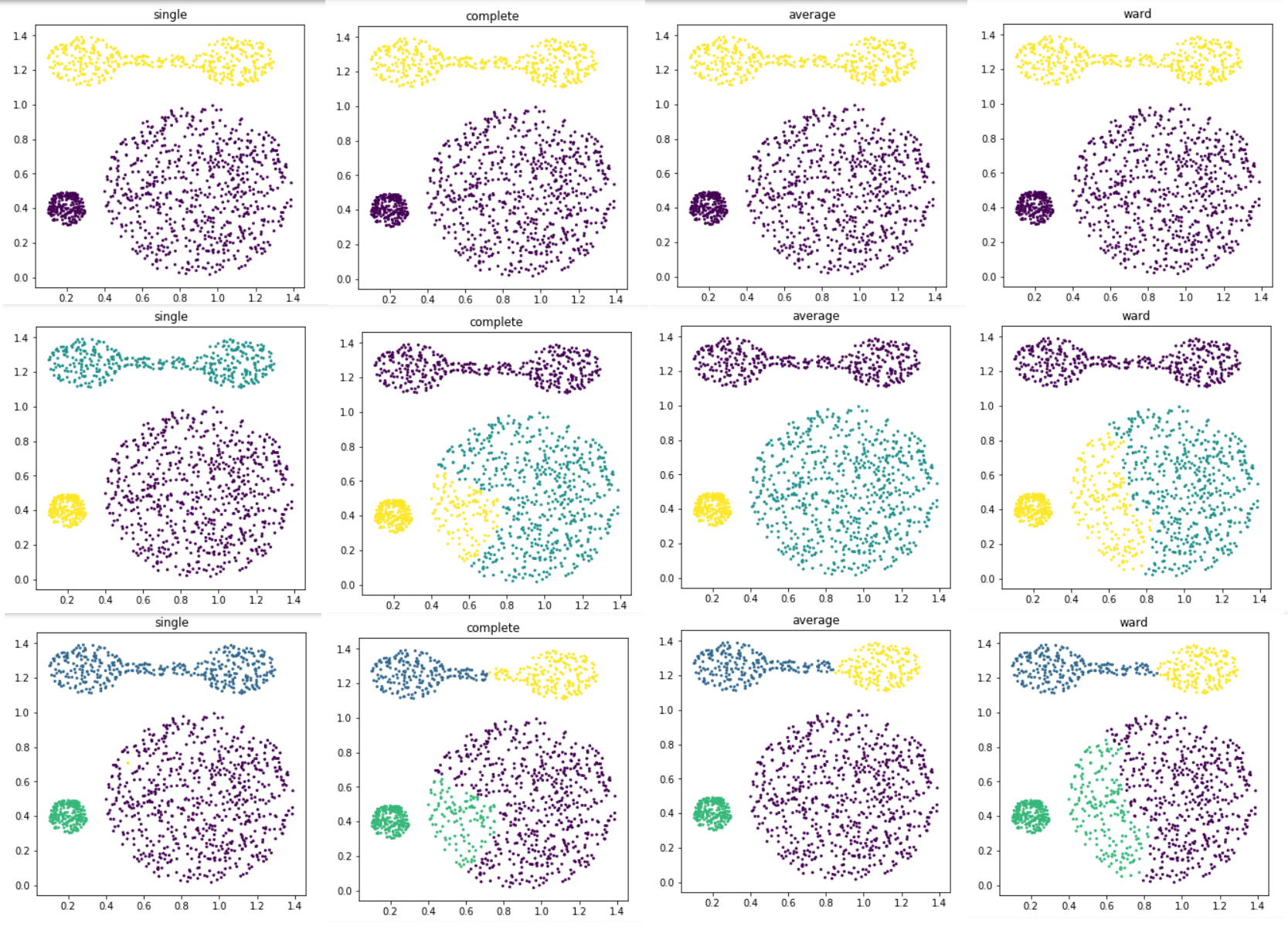
- distance를 single, complete, average, ward를 사용하고 각 distance에 대해서 cluster개수를 2부터 4까지 변경하면서 클러스터링을 해보고, 각각 결과를 visualization 하는 python code를 만들어 보시오
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
X = df.values
for num in range(2,5):
for i, linkage in enumerate(('single', 'complete','average', 'ward')):
clustering = AgglomerativeClustering(linkage=linkage, n_clusters=num)
y_pred = clustering.fit_predict(X)
plt.figure(i + 1, figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y_pred, s=4)
plt.title(linkage)
plt.show()
- 결과(2, 3, 4순서)
K-means Clustering(k-평균 클러스터링)
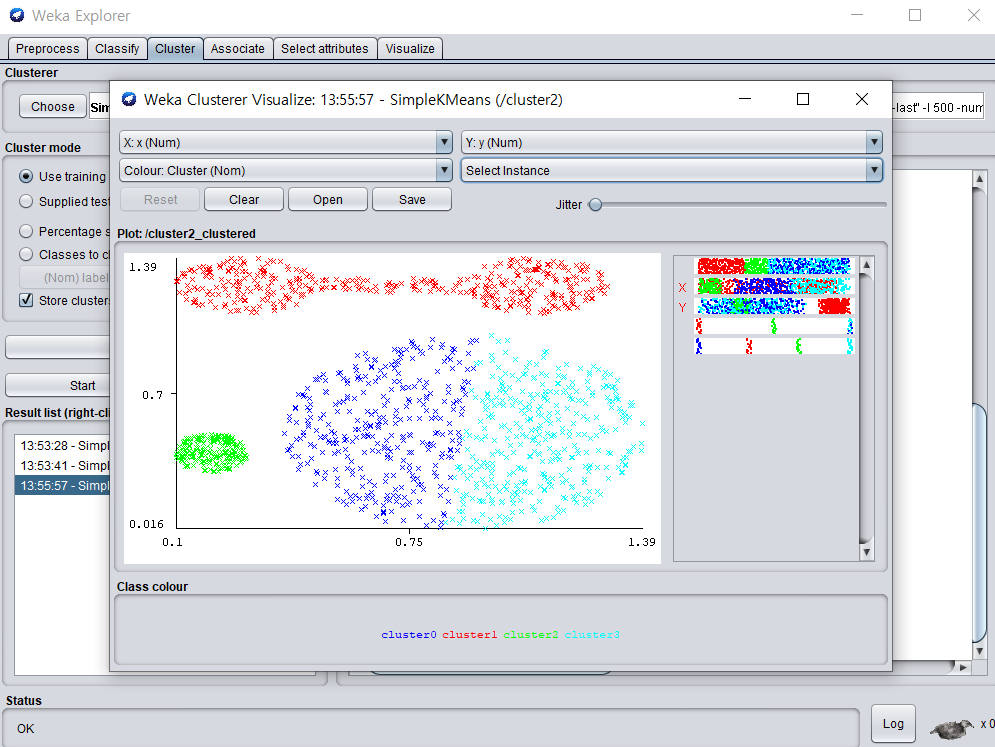
- weka를 이용한 simple kmeans
1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
X = df.values
k_means = KMeans(n_clusters=4, random_state=0)
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],
c=y_pred, s=4)
# 'c' : The color of each point
plt.show()
DBSCAN Clustering Algorithms
- Density-Based Clusterting Algorithms
- 데이터가 밀집한 정도 즉 밀도를 이용하여 클러스터의 형태에 구애받지 않으며 클러스터의 갯수를 사용자가 지정할 필요가 없다.
-
DBSCAN 방법에서는 초기 데이터로부터 근접한 데이터를 찾아나가는 방법으로 클러스터를 확장
- weka에서 dbscan install
- epsilon εε: 이웃(neighborhood)을 정의하기 위한 거리
- 최소 데이터 갯수(minimum points): 밀집지역을 정의하기 위해 필요한 이웃의 갯수
1
2
3
4
5
6
7
8
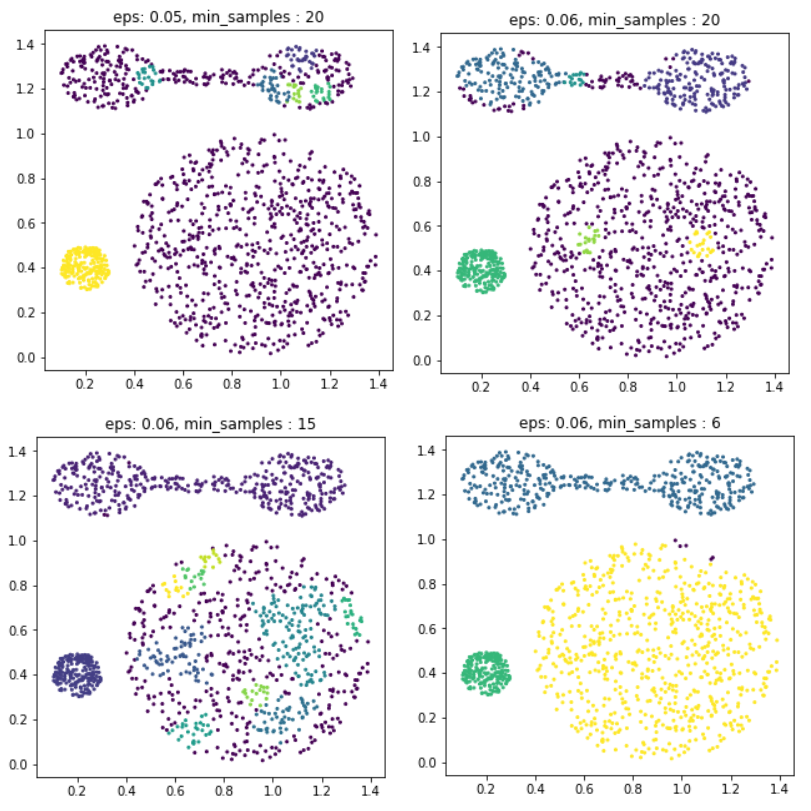
for i, (eps, min_samples) in enumerate(((0.05, 20), (0.06,20), (0.06,15), (0.06,6))):
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
y_pred = dbscan.fit_predict(X)
plt.figure(i + 1, figsize=(5,5))
plt.scatter(X[:,0], X[:,1], c=y_pred, s=4)
plt.title(f"eps: {eps}, min_samples : {min_samples}")
plt.show()
EM Clustering Algorithm(기댓값 최대화 알고리즘)
- Assume the data we have is sampled according to the generative model
- 몇개의 모수에 대한 초기값을 추정하는 것으로 시작하여 이 모수를 이용해 각각의 데이터가 군집에 속할 확률을 계산
- 각 클러스터의 값, 평균, 분산, 정규분포, 필요에 따라 확률분포
-
Log likehood
- 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from sklearn.mixture import GaussianMixture
em = GaussianMixture(n_components=4, max_iter=20, random_state=0)
y_pred = em.fit_predict(X)
# 클러스터의 사이즈와, 개수를 예상할 수 있음
print(em.weights_)
>>> [0.54305501 0.15217282 0.15989176 0.14488041]
# 클러스터 중심의 위치
print(em.means_)
>>> [[0.90092247 0.49695211]
[0.20256314 0.40738658]
[0.37381659 1.25479151]
[1.07851102 1.24600705]]
# 클러스터의 모양 -분산 정보(2차원)
print(em.covariances_)
>>> [[[ 6.49289207e-02 -4.78095962e-04]
[-4.78095962e-04 6.03293794e-02]]
[[ 2.73531910e-03 -7.02052996e-05]
[-7.02052996e-05 2.51901315e-03]]
[[ 3.12803346e-02 -5.83851370e-04]
[-5.83851370e-04 4.11677639e-03]]
[[ 1.44971509e-02 4.61343042e-04]
[ 4.61343042e-04 5.12229085e-03]]]
plt.figure(figsize=(5,5))
plt.scatter(X[:,0],X[:,1],
c=y_pred, s=4)
# 'c' : The color of each point
plt.show()
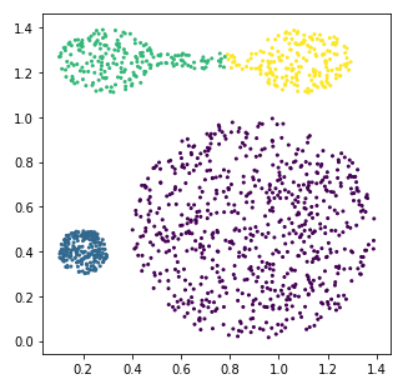
- 결과
PLSI(Probabilistic Latent Semantic Indexing)
- 문서마다 k개의 주제를 정해놓고 각 단어마다 단어에 가장 적합한 주제를 선택
Matrix Factorization
- Content based filtering method
- item이나 product등과 같은 actual content를 이용함
- 각 item간의 similarity를 이용해서 추천
- Collaborative filtering method
- 각각의 유저는 비슷한 다른 유저와 동일하게 행동한다는 가정, 다른 유저들이 추천에 영향을 끼침
- User가 직접 점수를 매긴 item들에 대한 rating을 이용해 추천
- Memory based method
- 과거의 rating에 기반해 rating predctions을 함
- rating 평가를 보고 비슷한, 유사한걸 찾음
- Model based method
- User database를 이용해서 predication을 위한 model을 생성
- 모델을 만들어서 그 모델을 평가
- Matrix Factorization이 여기에 해당
Matrix Factorization
- MF 모델은 user-item 의 matrix에서 이미 rating이 부여되어 있는 상황을 가정한다. (당연히 sparse한 matrix를 가정한다)
- MF의 목적은, Matrix Complement 이다.
- 아직 평가를 내리지 않은 user-item의 빈 공간을 Model-based Learning으로 채워넣는 것을 의미한다.