자료구조와 알고리즘 18강

18강: 이진 트리(Binary Tree)

이진 트리(Binary Tree)란?

이진트리는, 트리에 포함되는 모든 노드의 차수가 2 이하인 트리를 말한다
즉, 모든 노드는 자식이 없거나(리프 노드의 경우), 하나만 있거나, 아니면 둘 있는 세 경우 중 하나에 해당
트리는 정의 자체가 재귀적이기 때문에, 이를 대상으로 하는 연산들도 대부분 재귀적으로 구현이 가능하다
- size() - 현재 트리에 포함되어 있는 노드의 수를 구함
- depth() - 현재 트리의 깊이 (또는 높이)를 구함
트리의 각 노드를 정해진 순서로 방문하는 것을 **순회(traversal, search)연산 **이라고 부른다

이진 트리의 추상적 자료구조

연산의 정의

size()
depth()
순회(traversal, search)

구현

# Node
class Node:
    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

# Tree
class BinaryTree:
    def __init__(self, r):
        self.root = r

size()

재귀적인 방법으로 쉽게 구할 수 있음
전체 이진 트리의 size() = left subtree의 size + right subtree의 size + 1(자기 자신)

class Node:
  	# 자기 자신이 root인 subtree의 size를 구하는 멤버 메소드
    def size(self):
        # left subtree
        l = self.left.size() if self.left else 0
        # right subtree
        r = self.right.size() if self.right else 0
        return l + r + 1
      
class BinaryTree:
    def size(self):
        if self.root:
            return self.root.size()
        else:
            # empty tree
            return 0

depth()

재귀적으로
전체 이진 트리의 depth() = left subtree depth 와 right subtree depth 중 더 큰것 + 1

class Node:
    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        if(l >= r):
            return l + 1
        else:
            return r + 1 
          
class BinaryTree:
    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0

순회(Traversal, search)

깊이 우선 순회(Depth First Search, DFS)
- 이진 트리를 대상으로 하는 경우에는 세 가지의 서로 다른 순서를 정의할 수 있다.
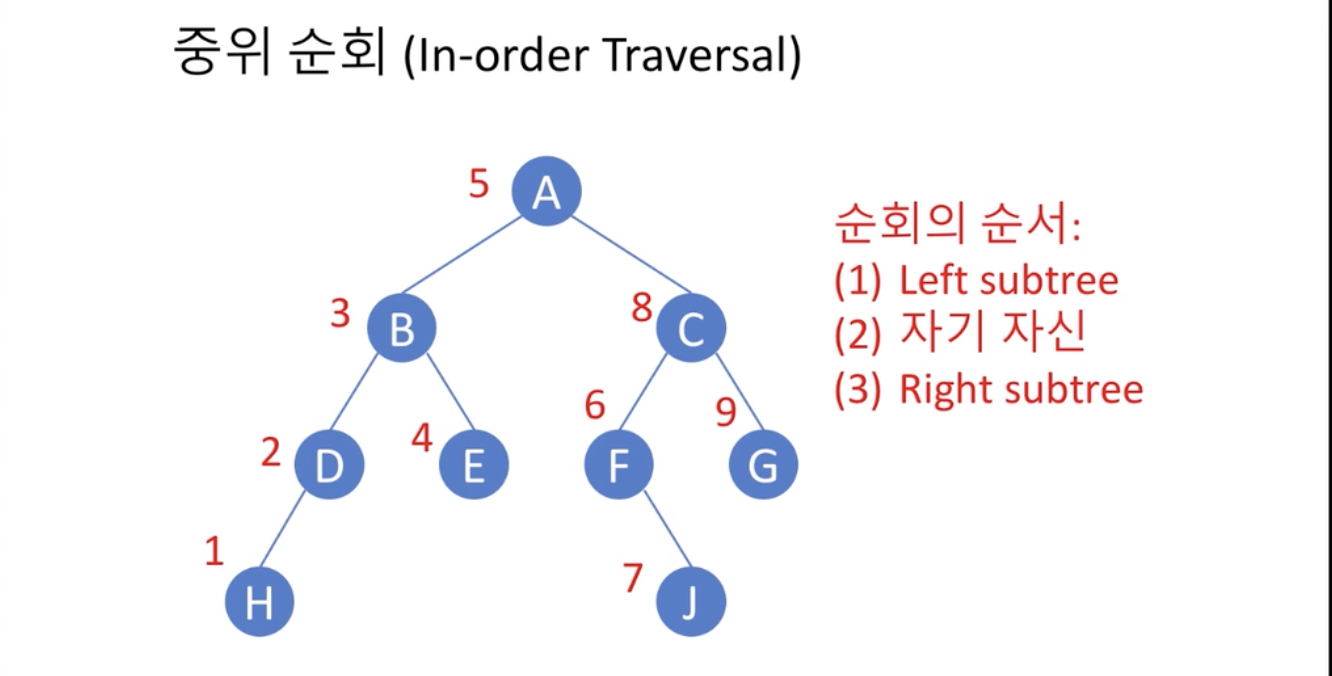
- 중위 순회(in-order traversal)
  - 왼쪽 서브트리를 순회한 뒤 노드 x를 방문, 그리고 나서 오른쪽 서브트리를 순회
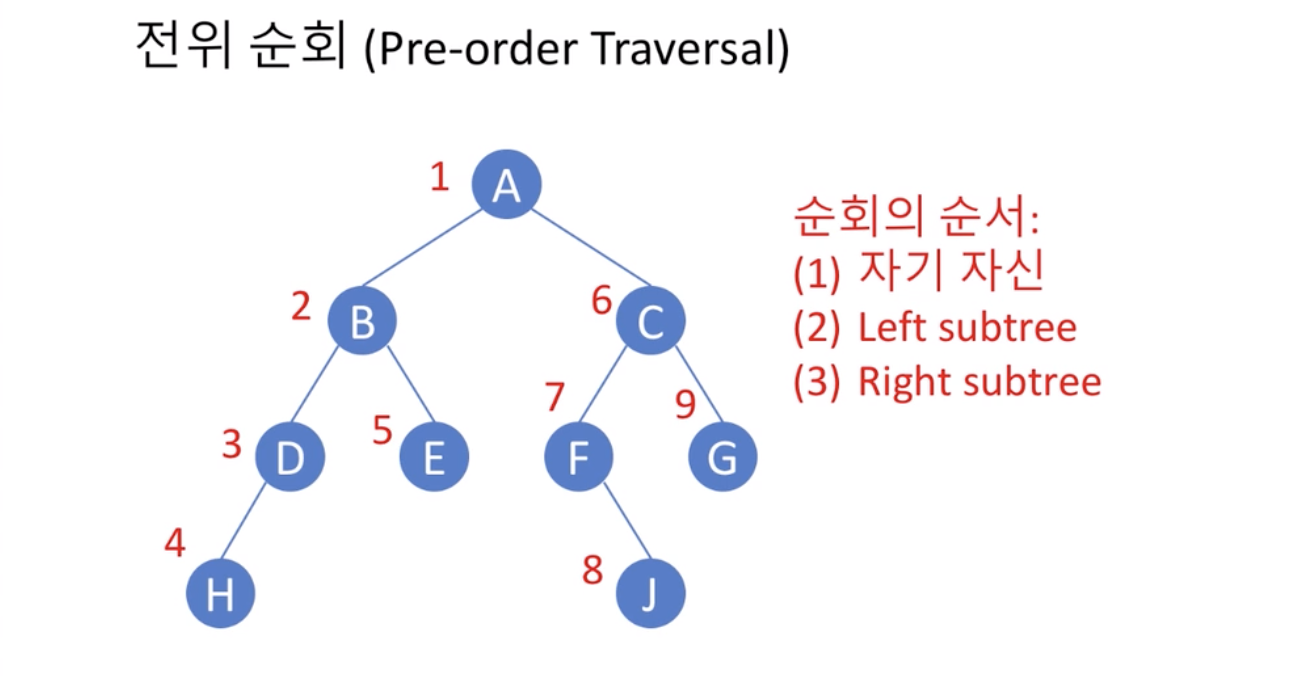
- 전위 순회(pre-order traversal)
  - 노드 x를 방문한 후에 왼쪽 서브트리를 순회, 마지막으로 오른쪽 서브트리를 순회
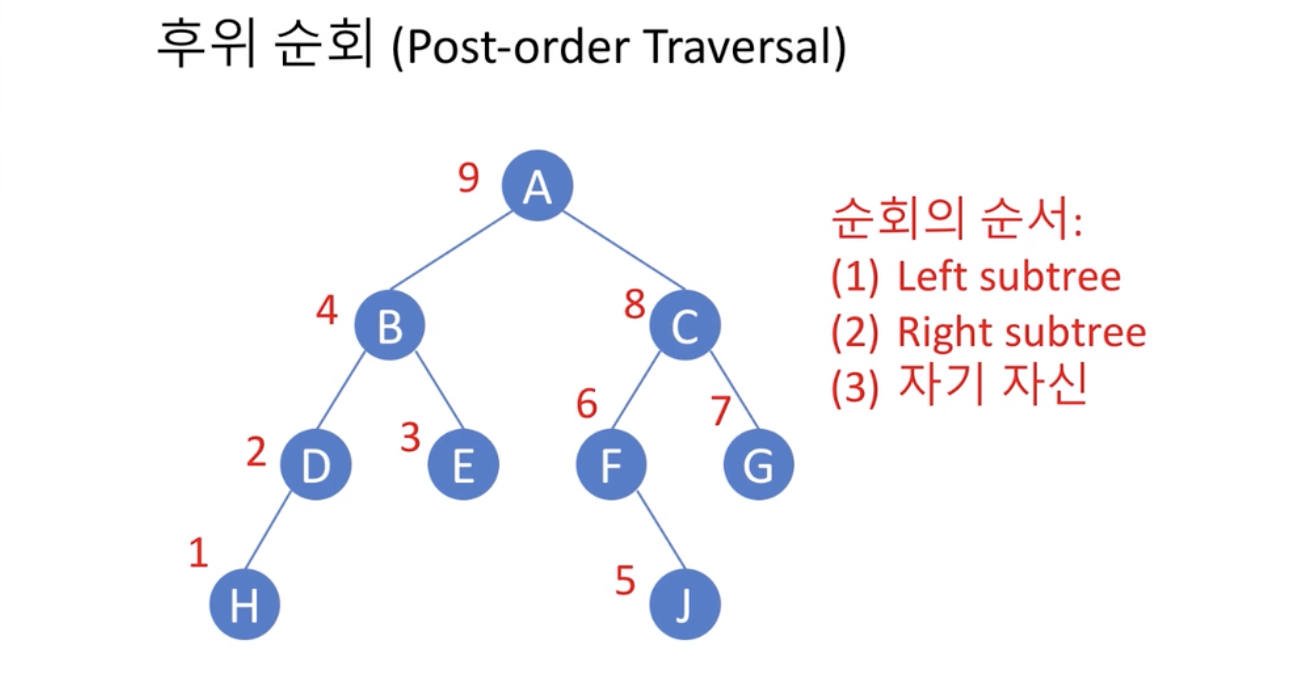
- 후위 순회(post-order traversal)
  - 왼쪽 서브트리를 순회, 오른쪽 서브트리를 순회, 그리고 나서 마지막으로 노드 x를 방문
넓이 우선 순회(Breadth First Search, BFS)

중위 순회(In-order Traversal)
1. Left subtree
2. 자기자신
3. Right subtree

in-order

class Node:
  	# 자기 자신을 루트로 하는 subtree에 대한 inorder traversal을 재귀적으로 
    def inorder(self):
        traversal = []
        # left subtree가 있으면
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self.data)
        # right subtree가 있으면
        if self.right:
            traversal += self.right.inorder()
        return traversal
      
class BinaryTree:
    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

전위 순회(Pre-order Traversal)
1. 자기자신
2. Left subtree
3. Right subtree

pre-order

class Node:
    def preorder(self):
        traversal = []
        traversal.append(self.data)
        if self.left:
            traversal += self.left.preorder()
        if self.right:
            traversal += self.right.preorder()
        return traversal
 
class BinaryTree:
    def preorder(self):
        if self.root:
            return self.root.preorder()
        else:
            return []

후위 순회(Post-order Traversal)
1. Left subtree
2. Right subtree
3. 자기자신

post-order

class Node:
    def postorder(self):
        traversal = []
        if self.left:
            traversal += self.left.postorder()
        if self.right:
            traversal += self.right.postorder()
        traversal.append(self.data)
        return traversal

class BinaryTree:
    def postorder(self):
        if self.root:
            return self.root.postorder()
        else:
            return []

본 문서는 프로그래머스 어서와! 자료구조와 알고리즘 강의를 수강하고 정리했습니다.

출처 : 프로그래머스 : 어서와! 자료구조와 알고리즘은 처음이지?

자료구조와 알고리즘 18강

자료구조와 알고리즘 18강

18강: 이진 트리(Binary Tree)

이진 트리(Binary Tree)란?

이진 트리의 추상적 자료구조

연산의 정의

구현

size()

depth()

순회(Traversal, search)

FEATURED TAGS

FRIENDS